Expansion and factorisation of quadratic equations
Hi, this is my blog on Expansion & Factorisation of Quadratic Expressions. First, let's start with some basics.

Did you know? The name Quadratic comes from "quad" meaning square, because the variable gets squared (like x2).
a, b and c are known values. a can't be 0.
 This is one example of how to solve a quadratic equation.
This is one example of how to solve a quadratic equation.Here are some examples of quadratic equations. Try filling in the blanks and solving them yourself!
------------------------------------------------------------------------------
Now, let's move on to expansion and factorisation.
What is expansion?
We are taking terms out of brackets.
E.g. 1
3z(z+y-4)-(y+3)(z+1)
=(3z^2+3zy-12z)-(zy+y+3z+3)
=3z^2+3zy-12z-zy-y-3z-3
=3z^2+2zy-12z-y-3
E.g. 2
-(2+g-g^2)+(6g-g^2)
=-2-g+g^2+6g-g^2
=-2+5g
Let's practice!
---------------------------------------------------------------------
Find what to multiply to make the Quadratic Equation
You need to put common factors outside and put the rest in brackets.
Factorise Single brackets
- Factorise brackets by dividing out a common factor from each term
Factorise a Quadratic
- List the factors of the constant term & select the pair which add to the coefficient of x.
Factorise a2 + 7a + 10
Factorise a2 - 2a - 8
Quadratics with a common factor
- Always check for a common factor which can be divided out first
| Factorise 3a2 - 9a - 30 | |
 |  |
 |  |
The difference between squares
- Two squares subtracted can be factorised easily
| Factorise a2 - 81 | ||
 |  | |
| Factorise 16a4 - 49y2 | ||
 |  | |
Factorised Quadratics
- A factorised quadratic is solved by making each bracket = 0
| ||||||
------------------------------------------------------------------------------
What is the difference?
Factorisation can be like trying to find out what ingredients went into a cake to make it so delicious. which is sometimes not obvious at all!
Let's practice!Easy? Let's have a test!
Now, let's combine these two concepts!

Did you get it? If you did, apply the concept to your exercises.
If not, then check out this video. It will surely help!
------------------------------------------------------------------------------
Just plug in the values of a, b and c, and do the calculations.
Now, you are probably like this:
Ok relax, we will do it step by step.
First of all what is that plus/minus thing that looks like ± ?
The ± means there are TWO answers:
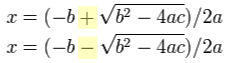
But sometimes you don't get two real answers, and the "Discriminant" shows why ...
Discriminant
Do you see b2 - 4ac in the formula above? It is called the Discriminant, because it can "discriminate" between the possible types of answer:
|
Just put the values of a, b and c into the Quadratic Formula, and do the calculations.
Example: Solve 5x² + 6x + 1 = 0
Here, 5 is a,6 is b and 1 is c.
Still don't get it? Here's a song to show you.
------------------------------------------------------------------------------
------------------------------------------------------------------------------
My reflections...
------------------------------------------------------------------------------
Now, don't you feel like...
Congratulations! You just learnt everything about Expansion & Factorisation of Quadratic Expressions!
Thank you and God bless!
Huang Tian Rui 2014































0 Comments:
Post a Comment
Subscribe to Post Comments [Atom]
<< Home